Tra gli elementi non strutturali, le tamponature in un edificio rivestono un ruolo fondamentale poiché isolano lo spazio interno da quello esterno, assolvendo alla funzione di “chiusura” di una costruzione.
Come già evidenziato nell’articolo precedente, il progettista è obbligato a verificare che tali elementi non influiscano sulla prestazione della struttura, garantendo sempre un margine di sicurezza a seguito di eventi sismici.
Ai fini della progettazione è necessario individuare un modello di calcolo che permetta di valutare correttamente le sollecitazioni agenti e procedere alle relative verifiche. Trattandosi di elementi bi-dimensionali realizzati con materiali ben lontani da essere considerati omogenei ed isotropi, è necessario fare ricorso a modelli semplificati.
Di seguito saranno analizzati dei modelli più comunemente utilizzati nella pratica professionale e, come vedremo, implementati in IperSpace BIM.
Comportamento dinamico della tamponatura
Per determinare l’accelerazione sismica, con la quale effettuare le verifiche di sicurezza, è necessario conoscere il periodo proprio di vibrazione Ta della tamponatura, che può essere schematizzata, in maniera semplificata, attraverso una trave a una mensola o su due appoggi, in base all’effettivo grado di vincolo in situ.
A sua volta, per l’analisi del comportamento dinamico la trave-tamponatura può essere trattata come un sistema continuo, del quale, attraverso lo studio del comportamento in caso di oscillazioni libere, si possono determinare la frequenza fondamentale, il periodo associato e le forme modali.
Adottando per la tamponatura una schematizzazione a trave con rigidezza flessionale EI e massa per unità di lunghezza μ=Aρ, con A area della sezione trasversale e ρ densità di massa, il comportamento dinamico si può valutare considerando la stessa come un sistema continuo, la cui equazione di equilibrio in condizione di oscillazioni libere si scrive:

Introducendo l’autofunzione Ψ(x), l’equazione differenziale che governa il problema diventa:
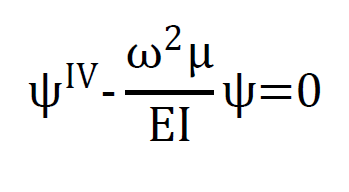
Il cui integrale generale è:
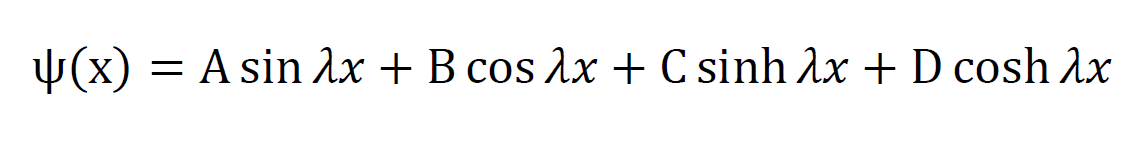
essendo A,B,C e D opportune costanti determinabili dalla scrittura delle equazioni al contorno e avendo posto
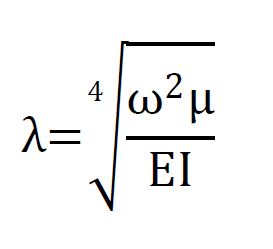 La scrittura delle equazioni al contorno fornisce un sistema di quattro equazioni nelle quattro incognite A, B, C e D. Affinché tale sistema abbia soluzioni diversa da quella banale deve essere nullo il determinante della matrice dei coefficienti. Imponendo tale condizione si determinano le frequenze del sistema continuo.
La scrittura delle equazioni al contorno fornisce un sistema di quattro equazioni nelle quattro incognite A, B, C e D. Affinché tale sistema abbia soluzioni diversa da quella banale deve essere nullo il determinante della matrice dei coefficienti. Imponendo tale condizione si determinano le frequenze del sistema continuo.
Le equazioni risolutive sono:
- nel caso di trave a mensola:

- nel caso di trave appoggiata:

Si tratta di equazioni trascendenti nell’incognita λL che posseggono infinite radici. Per la radice n-esima si può ricavare la corrispondente frequenza, il relativo periodo, e dalla soluzione del sistema omogeneo l’autofunzione associata, rappresentativa della deformata modale.

I risultati sono indicati nella tabella seguente:

Le autofunzioni, calcolate per i primi quattro valori delle frequenze, sono riportati nelle immagini seguenti. Tali funzioni rappresentano, per le tipologie di travi esaminate, l’andamento delle deformate modali.

In merito alle tamponature, “nella verifica di meccanismi locali in edifici multipiano è, in genere, sufficiente riferirsi al solo primo modo di vibrare nella direzione di verifica, in quanto è quello che induce la domanda di spostamento più significativa” [Circolare 2019, §C7.2.3].
Di conseguenza si valuta direttamente la frequenza a il periodo primo in corrispondenza della prima radice delle equazioni riportate in precedenza. Quindi:
- Trave incastrata ad un estremo

- Trave appoggiata agli estremi

Nel caso in cui si voglia schematizzare la tamponatura come una lastra rettangolare di dimensioni HxL e spessore t appoggiata sui quattro lati, la trattazione analitica risulta molto più complessa. Si riportano di seguito direttamente le formulazioni delle grandezze di interesse ai fini dell’analisi in esame.
La pulsazione naturale relativa al primo modo di vibrare si esprime come:

Dove D è la rigidezza flessionale della lastra:

con E e ν rispettivamente modulo elastico e coefficiente di Poisson del materiale.
Verifica della tamponatura
Anche ai fini della verifica fuori piano, una tamponatura di altezza h, spessore t e lunghezza L, può essere considerato come una trave di sezione trasversale b x t, vincolata come una mensola oppure mediante due appoggi.
Il comportamento fuori piano delle tamponature, che sono inserite all’interno del telaio strutturale, dipende dall’efficienza del vincolo che si riesce ad ottenere, mediante dettagli costruttivi, lungo il bordo. A tal proposito di individuano essenzialmente due tipologie di meccanismo fuori piano:
- Flessione verticale, qualora la tamponatura sia vincolata alla trave superiore e quella inferiore (modello di trave su due appoggi) e in tal caso il collasso avviene a seguito della formazione di un meccanismo ad arco;
- Ribaltamento fuori piano con rotazione della tamponatura intorno alla base, qualora questa sia vincolata solo alla trave inferiore (modello di trave a mensola);

In entrambi i casi è stato trascurato il vincolo laterale con i pilastri.
L’azione sismica si schematizza come un carico uniformemente distribuito, e in base alla condizione di vincolo, il massimo momento sollecitante risulta essere pari a:
- Ms=1/8∙qH2 per la schematizzazione di trave su due appoggi;
- Ms= 1/2∙qH2 nel caso di trave a mensola.

Per il calcolo del momento resistente si effettua l’equilibrio alla traslazione e alla rotazione della sezione trasversale, ipotizzando un diagramma delle tensioni di compressione rigido-plastico (stress-block) in modo del tutto analogo a quanto effettuato per la verifica di pareti in muratura.
Tale momento resistente MR si valuta come:
 Dove:
Dove:
- l è la lunghezza della tamponatura;
- t è lo spessore della tamponatura
- σ0 è la tensione normale media, riferita all’area totale della sezione, σ0 = N/(Lt), con N forza assiale di compressione
- fd la resistenza a compressione di progetto del materiale che costituisce la tamponatura.

