La validazione del codice di calcolo dei software è necessaria per attestare la veridicità dei risultati ottenuti. Le NTC 2018 al paragrafo 10.2 riportano diverse considerazioni in merito:
Qualora l’analisi strutturale e le relative verifiche siano condotte con l’ausilio di codici di calcolo automatico, il progettista, dovrà controllare l’affidabilità dei codici utilizzati e verificare l’attendibilità dei risultati ottenuti. Il progettista dovrà quindi esaminare preliminarmente la documentazione a corredo del software per valutarne l’affidabilità e soprattutto l’idoneità al caso specifico. In tal senso la documentazione, che sarà fornita dal produttore o dal distributore del software, dovrà contenere una esauriente descrizione delle basi teoriche e degli algoritmi impiegati, l’individuazione dei campi d’impiego, nonché casi prova interamente risolti e commentati, per i quali dovranno essere forniti i file di input necessari a riprodurre l’elaborazione.
In questo approfondimento viene analizzata la validazione del codice di calcolo utilizzato nel software Bulk facendo riferimento all’esempio 13.3 del libro Fondazioni – Progetto e Analisi (Bowles, 1991, McGraw Hill Education).
Validazione di Bulk: analisi lineare
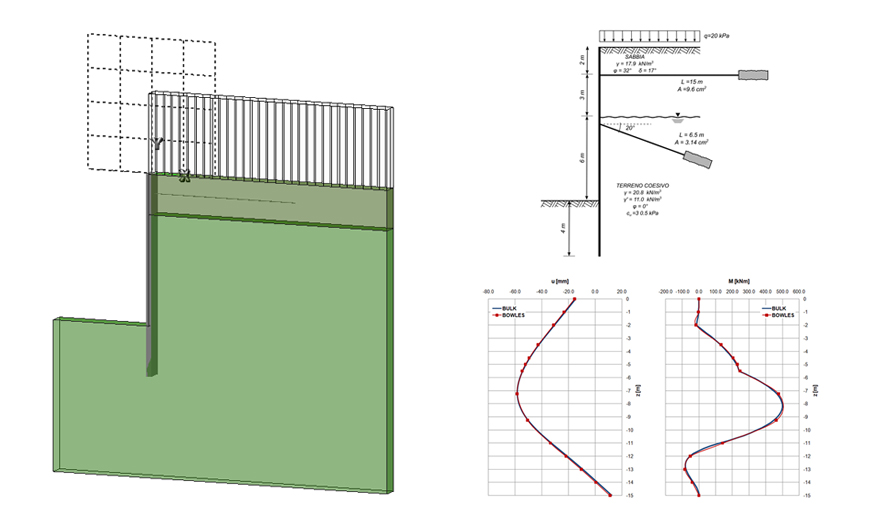
Una paratia di acciaio, lunga 15 metri, sorregge un terrapieno di sabbia, il cui spessore è pari a 5 metri, sovrastante uno strato di argilla. La profondità d’infissione è assunta pari a 11 metri e sono presenti due barre di ancoraggio: la prima orizzontale, a quota pari a 2 metri, disposta sopra il livello dell’acqua e la seconda inclinata di 20° rispetto all’orizzontale, disposta a quota 5,5 metri rispetto al piano campagna. Il piano di falda coincide con l’inizio dello strato di argilla. Si assume che, a monte della paratia, agisca un carico distribuito nastriforme pari a 20 kPa.
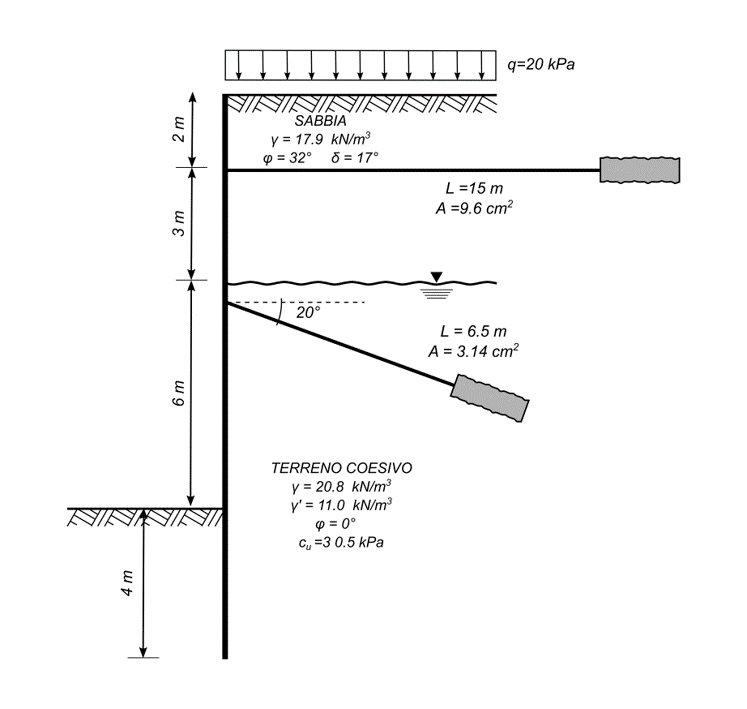
La procedura di calcolo agli elementi finiti consiste nel modellare il terreno in corrispondenza della linea di fondo scavo come una serie di molle, di rigidezza ks applicate alla paratia, che contribuiscono alla resistenza allo spostamento; la spinta attiva del terreno, calcolata attraverso il coefficiente di spinta Ka, le eventuali spinte idrostatiche e quelle dovute ai carichi esterni, si considerano applicate fino alla linea di fondo scavo.
Per l’applicazione del metodo proposto da Bowles è necessario, preliminarmente:
- discretizzare la paratia, stabilendo la posizione dei nodi di analisi. I parametri necessari al calcolo sono solo il momento d’inerzia e il modulo di elasticità;
- diagrammare le spinte a tergo della paratia e valutarne la risultante, in corrispondenza di ogni nodo;
- assegnare ai nodi in corrispondenza del terreno, all’interno del quale la paratia è infissa, la relativa rigidezza calcolata sulla base dello spostamento di plasticizzazione Δ, attraverso la relazione:
![\[ k_{s}=\frac{q_{lim}}{\Delta} \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-74b1add7867a54ff6f0f830ef0014ba0_l3.png "Rendered by QuickLaTeX.com")
- assegnare la rigidezza ai nodi in corrispondenza degli ancoraggi.
La sostanziale differenza tra la procedura proposta da Bowles e quella implementata in Bulk è che la spinta del terreno, la rigidezza delle molle e dei tiranti non sono implementate dall’utente, ma calcolate in automatico a partire dalle geometrie degli elementi e dalle caratteristiche meccaniche e fisiche dei terreni.
Pertanto, al fine di confrontare i risultati ottenuti dalla modellazione del problema attraverso Bulk con quelli ricavati da Bowles, è necessario adottare le stesse ipotesi semplificative utilizzate da quest’ultimo:
- La rigidezza ks delle molle al di sotto della linea di fondo scavo è considerata constante lungo l’altezza e pari al valore assunto in corrispondenza del piano campagna. Tale assunzione è ragionevole poiché, per argille normal-consolidate (φ ≈ 0), l’aliquota del carico limite dovuta alla coesione risulta essere preponderante rispetto agli altri termini. Si trascura, quindi, l’incremento di ks con l’aumentare della profondità.
![\[ k_{s}=\frac{q_{lim}}{\Delta}=7320\frac{kN}{m^{3}} \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-141758eb3eb5dcef330c1f46a7836974_l3.png "Rendered by QuickLaTeX.com")
essendo:
![\[ q_{lim}=N_{q}\cdot\gamma\cdot z+N_{c}\cdot c \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-a1236631ce3433789f79b5bcdd80e592_l3.png "Rendered by QuickLaTeX.com")
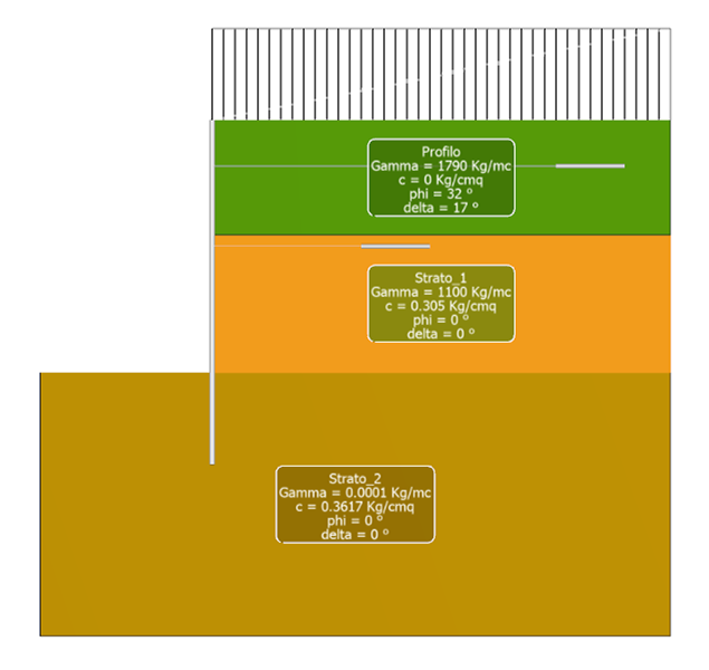
Poiché Bulk calcola la rigidezza delle molle a partire dai dati relativi alle caratteristiche fisiche e meccaniche del terreno (γ e φ), è necessario considerare il terreno al di sotto della linea di fondo scavo senza peso, ma resistente. Ciò si traduce nell’assegnare al peso specifico un valore tendente a zero (nel caso in esame 0,0001 kN/m3). Risulta, quindi:
![\[ q_{lim}=N_{c}\cdot c \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-f76161af01fb007d8aaa215968c7fc8d_l3.png "Rendered by QuickLaTeX.com")
Esplicitando l’espressione di Ks e assumendo lo spostamento di plasticizzazione pari a 2,54 cm, si ottiene il valore da assegnare alla coesione del terreno:
![\[ k_{s}=\frac{N_{c}\cdot c}{\Delta}=7320\frac{kN}{m^{3}}\rightarrow c=\frac{k_{s}\cdot\delta}{N_{c}}=\frac{7320\cdot2,54\cdot10^{-2}}{5,14}=36,17\frac{kN}{m^{2}} \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-09cda86df9cb9e4306b4df9170e41971_l3.png "Rendered by QuickLaTeX.com")
- Si trascura l’effetto della spinta dell’acqua; pertanto, la modellazione è avvenuta escludendo la falda. Ciò significa che il peso dell’unità di volume da utilizzare non è quello saturo, pari a 20,8 kN/m3, ma quello efficace:
![\[ \gamma^{'}=\gamma_{SAT}-\gamma_{W}=11\frac{kN}{m^{3}} \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-f6e97a24489d32ed46afe742c655319f_l3.png "Rendered by QuickLaTeX.com")
- Il calcolo è effettuato considerando un tratto di paratia di lunghezza unitaria. A partire dal valore noto dell’inerzia, posta la larghezza della paratia B pari a 1 metro, si calcola il valore da assegnare all’altezza come segue:
![\[ I=\frac{B\cdot H^{3}}{12}=670\cdot10^{-6}m^{4}\rightarrow H=\sqrt[3]{\frac{12I}{B}}=\sqrt[3]{\frac{12\cdot670\cdot10^{-6}}{1}}=0,2m \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-2a5d3f212ddc16fd5ec91c39e939596c_l3.png "Rendered by QuickLaTeX.com")
La paratia è in acciaio, pertanto si assegna E=2∙109 kPa.
- Per i tiranti disposti all’interno del terreno con una certa inclinazione, la componente dell’azione interna che interessa è solo quella orizzontale. Poiché Bulk tiene conto anche degli effetti della componente verticale, è opportuno modellare il tirante come orizzontale.
Noti i valori di input della rigidezza assiale in corrispondenza dei tiranti, si calcolano i valori da assegnare al modulo di elasticità:
![\[ K_{1}=\frac{A\cdot E}{L}=3030\frac{kN}{m}\rightarrow E_{2}=\frac{K\cdot L}{A}=\frac{3030\cdot6,5}{3,14\cdot10^{-4}}=62,19\cdot10^{6}kPA \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-fbb4eeed31ba4447566246c54f43f948_l3.png "Rendered by QuickLaTeX.com")
Tutti gli accorgimenti sopra esposti risultano necessari affinché il modello di calcolo da realizzare in Bulk corrisponda a quello riportato dall’esempio proposto da Bowles. Si tenga presente, infine, che l’analisi deve essere condotta in ipotesi di linearità del comportamento delle molle e ponendo pari all’unità tutti i coefficienti parziali di sicurezza.
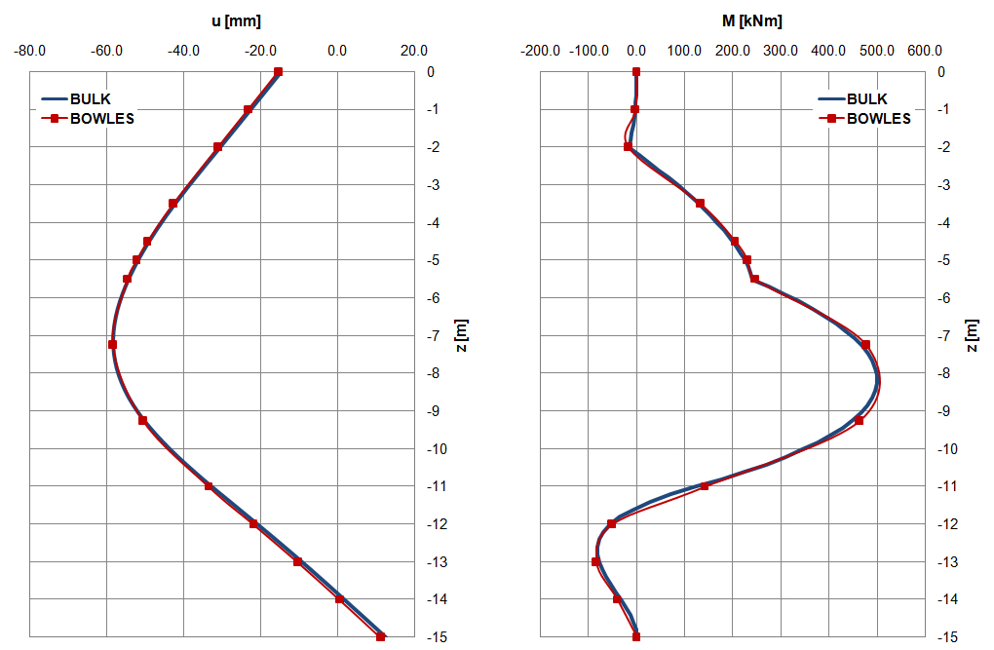
Dall’analisi dei risultati ottenuti (Figura 3), si può notare che i risultati ottenuti dal software coincidono con quelli di Bowles (Fondazioni, progetto e analisi – Figura 13.12d), a meno di piccole variazioni dovute ad una discretizzazione della paratia più fitta (77 elementi con un passo massimo di discretizzazione pari a 20 cm in Bulk, a fronte dei 13 elementi dell’esempio).
In corrispondenza della linea di fondo, lo spostamento calcolato dal software è pari a 32,8 mm, con una differenza di 0,8 mm (differenza del 2%) rispetto a quello riportato da Bowles. Il massimo valore del momento sulla struttura è pari a 499,7 kNm e si attinge ad una distanza dalla testa della paratia pari a 8,25 metri. Poiché l’esempio effettua una discretizzazione della paratia più grossolana il massimo momento, pari a 477,96 kNm si verifica ad una distanza dalla testa pari a 7,25 m.
È da osservare che molte delle ipotesi effettuate si sono rese necessarie affinché i dati di input tra i due modelli corrispondessero: l’esempio ha il solo scopo di effettuare un confronto tra i risultati ottenuti dal software.
L’analisi lineare è, infatti, una forzatura del reale comportamento del terreno in quanto spostamenti di 60 mm sono ben lontani dal comportamento elastico. La spinta idrostatica andrebbe considerata al fine di effettuare una modellazione più aderente alla realtà; così come gli ancoraggi, molto probabilmente, sono sotto-dimensionati.
Analisi non lineare
La validazione del codice di calcolo è avvenuta facendo riferimento all’esempio 13.1 del Libro Fondazioni – Progetto e Analisi [Bowles, 1991, McGraw Hill Education].
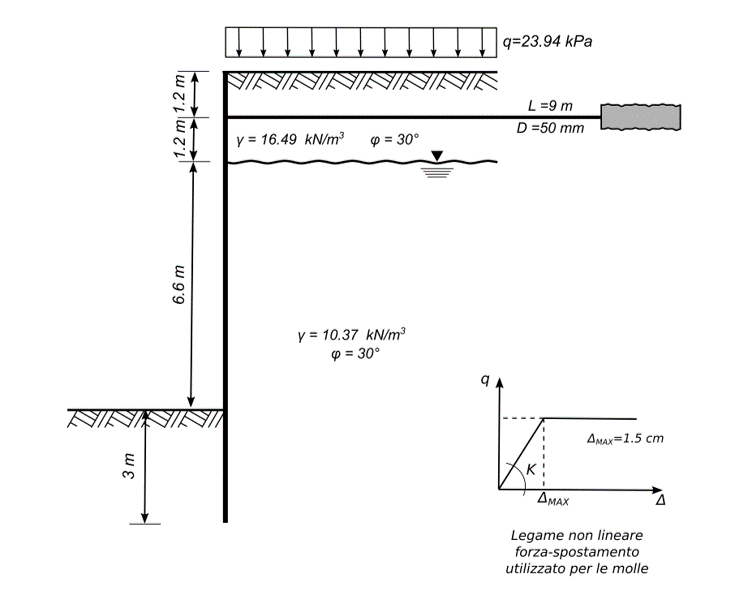
Una paratia di acciaio, lunga 12 metri, è disposta in un terreno incoerente. Il piano di falda è posto a quota 2,40 m; si stima γ = 16,47 kN/m3 al di sopra della superficie dell’acqua e γ = 10,37 kN/m3, l’angolo di attrito interno si assume pari a 30°.
La profondità di infissione è pari a 9 metri ed è presente una barra di ancoraggio orizzontale a 1,20 m dalla testa dell’opera. Si assume che, a monte della paratia, agisca un carico distribuito nastriforme pari a 23,94 kPa. Poiché il livello dell’acqua è lo stesso da entrambi i lati della paratia, la quale si considera permeabile in corrispondenza dei giunti, la sua presenza verrà ignorata nel calcolo della pressione attiva del terreno.
Si conduce un’analisi di tipo non lineare, assumendo come spostamento di plasticizzazione delle molle il valore 1,5 cm. Il calcolo è effettuato considerato una paratia di larghezza unitaria.
L’esempio proposto stima per il calcolo della spinta attiva il coefficiente Ka pari a 0,30 poiché il range di variabilità, in funzione di ogni ragionevole valore dell’angolo di attrito paratia-terreno δ è estremamente ridotto.
Tale valore di Ka= 0,30 si ottiene adottando la formulazione di Coulomb per il calcolo dei coefficienti di spinta, per un angolo di attrito δ pari a 0,16; pertanto, al fine di poter confrontare i risultati, la modellazione dei terreni in Bulk avviene considerando tale valore. Poiché la spinta dell’acqua nel calcolo è ignorata, si ommette l’inserimento della falda.
Le dimensioni della paratia sono state scelte in modo tale che l’inerzia coincida con quella utilizzata all’interno dell’esempio.
![\[ I=\frac{B\cdot H^{3}}{12}=255,56\cdot10^{-6}m^{4}\rightarrow H=\sqrt[3]{\frac{12I}{B}}=\sqrt[3]{\frac{12\cdot255,56\cdot10^{-6}}{1}}=0,145m \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-5669b6ab71b2b3705d9af8d865a55517_l3.png "Rendered by QuickLaTeX.com")
Analoga considerazione è stata effettuata per la determinazione del modulo di elasticità dell’acciaio del tirante.
![\[ K=\frac{A\cdot E}{L}=24240\frac{kN}{m}\rightarrow E=\frac{K\cdot L}{A}=\frac{24240\cdot9}{\pi\left(\frac{0,05}{2}\right)^{2}}=1,11\cdot10^{8}kPA \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-f7e9689c5938d5b5f1e32144adadee05_l3.png "Rendered by QuickLaTeX.com")
Un confronto fra i risultati ottenuti è riportato di seguito.
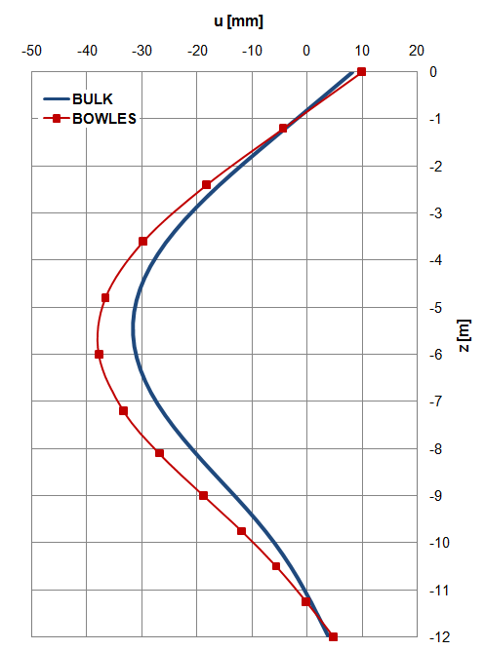
Come si può notare dal grafico di Figura 5, la paratia modellata in Bulk risulta essere più rigida rispetto a quella analizzata da Bowles. La principale motivazione è da ricercarsi all’interno dell’espressione utilizzata per la determinazione della rigidezza delle molle.
![\[ k_{s}=\frac{q_{lim}}{\Delta}=\frac{1}{\Delta}\left[N_{q}\cdot\gamma\cdot z+N_{c}\cdot c+N_{\gamma}\cdot\gamma\cdot\frac{B}{2}\right] \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-ed02323e1d923441e5e9dfc9da674a9f_l3.png "Rendered by QuickLaTeX.com")
L’espressione implementata all’interno di Bulk per la determinazione del coefficiente Nγ è quella proposta da Vesic (1973).
![\[ N_{\gamma}=2\left(N_{q}+1\right)\tan\varphi \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-4e6577a28733d2a09a3f6c7705571ede_l3.png "Rendered by QuickLaTeX.com")
che fornisce valori più elevati del 25% rispetto a quella proposta da Hansen (1970) e utilizzata all’interno dell’esempio di Bowles.
Un valore più elevato di Nγ fornisce valori più elevati del carico limite e, di conseguenza una maggiore rigidezza delle molle, cui corrisponde una minore deformabilità della paratia.
Inoltre, esplicitando l’espressione per il calcolo della rigidezza si ha:
![\[ k_{s}=\frac{N_{q}\cdot\gamma}{\Delta}\cdot z+\frac{N_{\gamma}\cdot\gamma\cdot\frac{B}{2}}{\Delta}=\frac{18,4\cdot10,37}{0,0015}z+\frac{22,4\cdot10,37\cdot0,5}{0,015}=7740z+12721 \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-29b737eaa616fb14ce3c693e39c816ef_l3.png "Rendered by QuickLaTeX.com")
valori molto più elevati rispetto a quelli dell’esempio originale, che utilizza:
![\[ k_{s}=7740z+11000 \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-d13d51776091273b2ffc9b8e57908219_l3.png "Rendered by QuickLaTeX.com")
Tali valori sono stati arrotondati nella versione italiana del libro al fine di renderli compatibili con quelli usati da Bowles nella versione originale che contenevano un errore di calcolo.
Tale discordanza di risultati, pertanto è dovuta a una differente valutazione della rigidezza delle molle.
Se si vuole fare in modo che le rigidezze combacino, che si ricorda sono inserite come valori di input all’interno dell’esempio, è necessario modificare i parametri di resistenza del terreno sotto la linea di fondo scavo.
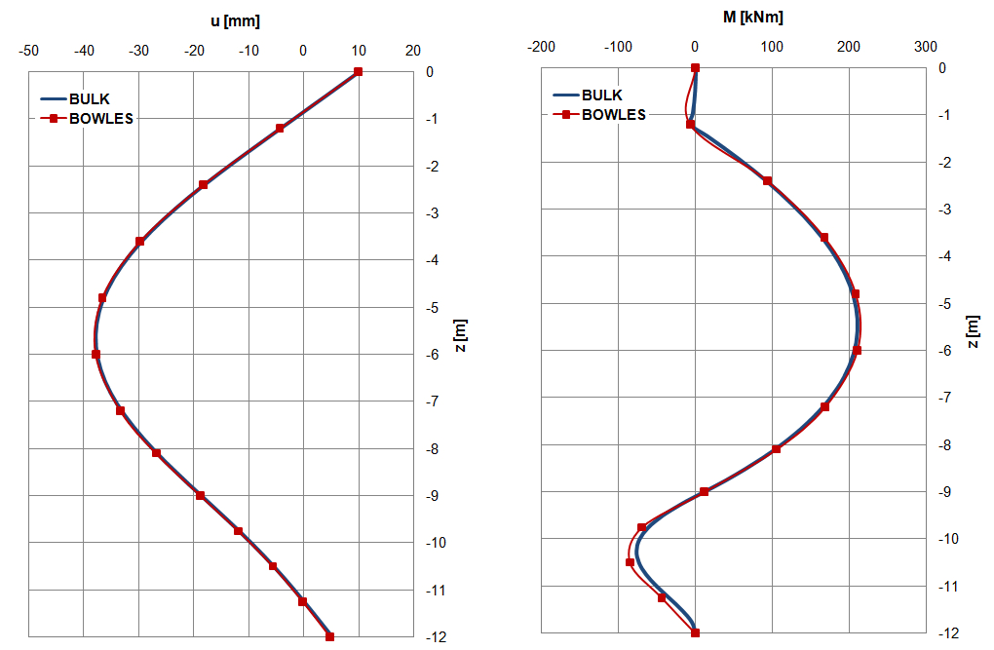
Utilizzando, a tal proposito, γ= 104,39 kN/m3 e φ=5,09° si ottiene la medesima espressione di Ks e, come si può notare dall’esame dei grafici di Figura 6, i risultati combaciano perfettamente.
È giusto ribadire, ancora una volta, che un terreno con tali caratteristiche è poco realistico; tale assunzione ha il solo scopo di poter effettuare un confronto e validare il codice di calcolo.
Scarica il .pdf de “La validazione del codice di calcolo del software per le paratie Bulk“.
Acquista Bulk il software per il calcolo lineare e non lineare e la verifica di paratie con assistenza e consulenza personalizzata inclusa. Per informazioni scrivi a comunicazione@soft.lab.it oppure chiama lo 0824.874.932
Leggendo la validazione del software ho notato che bulk inserisce uno spostamento di 1.5 cm per la plasticcizazione dele molle? E’ giusto considerare questo valore? Non e’ giusto inserire una relazione che e’ funzione della spinta passiva?
In Bulk, il comportamento del terreno è modellato attraverso molle caratterizzate da un legame elasto-plastico.
La rigidezza del tratto elastico è calcolata come carico limite diviso uno spostamento di plasticizzazione, il cui valore è scelto dall’utente. Analogamente l’utente può scegliere come valore massimo della resistenza della molla il carico limite, la resistenza passiva o il minimo fra i due.
Nell’esempio è stato scelto di considerare come spostamento di plasticizzazione il valore di 1,5 cm in modo che, per la validazione del software, i dati di ingresso corrispondessero esattamente a quelli previsti da Bowles nell’esempio come riferimento.
Buongiorno,
volevo chiedere quali valori di coefficienti di spinta attiva e passiva sono stati inseriti all’interno di bulk per la validazione nell’esempio di analisi non lineare.
Sono stati considerati su tutta l’altezza della paratia?
Grazie
I coefficienti di spinta vengono derivati dal software, e non inseriti direttamente dall’utente, così come la rigidezza delle
molle e dei tiranti, che sono quindi calcolate in automatico a partire dalle geometrie e dalle caratteristiche meccaniche e fisiche dei materiali e terreni.
Dunque i valori proposti da Bowles sono replicati agendo sulle proprietà che Bulk espone all’utente.
Ok grazie. Immagino che Bulk calcoli i coefficienti di spinta attiva e passiva mediante la definizione dell’angolo di attrito del terreno e del coefficiente di attrito muro-terreno: posso sapere che valori di delta avete considerato per il calcolo?
Inoltre, la rigidezza delle molle in Bulk viene calcolata in automatico cono scendo le caratteristiche di deformabilità del terreno? Se si, che valore di moduli elastici per i vari terreni avete considerato nel modello di validazione non lineare?
Grazie