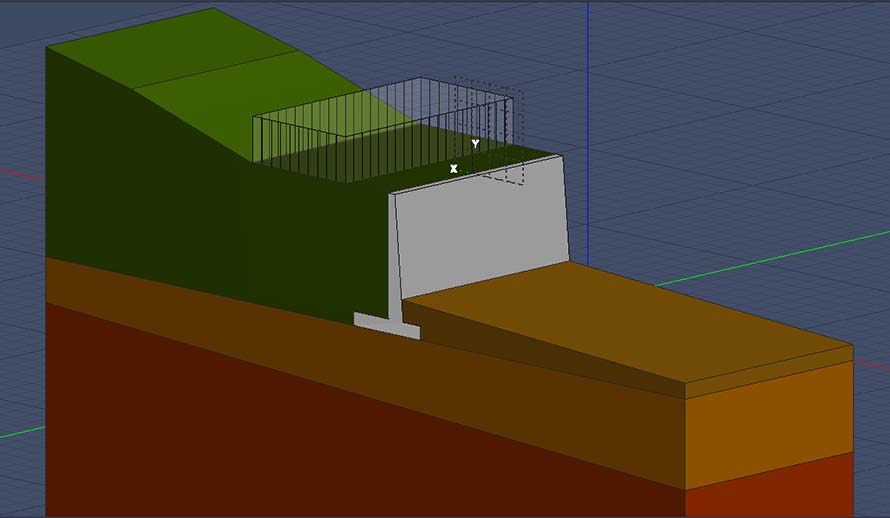
Le opere di sostegno sono delle strutture che vengono realizzate qualora si renda necessario contrastare i movimenti del terreno, sia esso di riporto che risultanti da uno scavo. Le tipologie di terreno vengono individuate in due macro categorie:
- Terreni privi di coesione (sabbia, ghiaia, etc)
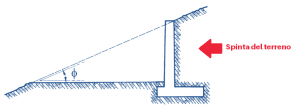
Dove φ rappresenta l’angolo di natural declivio (angolo di attrito interno)
- Terreni coesivi (argilla, limi, etc) esercitano una spinta sulle pareti di sostegno di entità inferiore a quella esercitata dai terreni incoerenti.
Tali tipologie di strutture si suddividono in rigide o flessibili in relazione al loro diverso grado di rigidezza, dipendente dal tipo di materiale che viene impiegato nella loro costruzione e dalle dimensioni che presentano. Le opere di sostegno rigide vengono di solito utilizzate per altezze relativamente basse per le altre si ricorre a quelle flessibili dotate di una certa deformabilità.
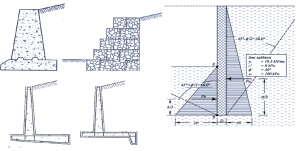
Tra le opere di sostegno rigide vanno menzionate i muri a gravità (di notevole spessore, si oppongono al terreno tramite il peso e ruotano rigidamente intorno ad un punto posto alla base), muri in cemento armato (anch’essi a gravità ma con una possibilità di deformazione maggiore) ed i muri a semigravità (dimensioni più ridotte della prima tipologia ma hanno un’armatura metallica).
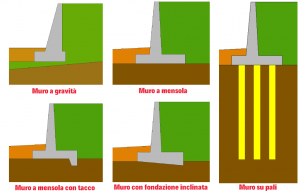
Durante la fase di progettazione dei muri di sostegno, siano essi rigidi o flessibili, è indispensabile una corretta definizione delle azioni esterne e delle condizioni al contorno.
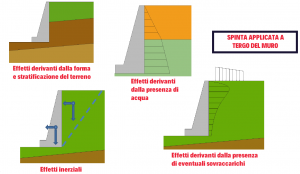
Se consideriamo il caso del muro ideale e volessimo calcolare la spinta infinitesima del terreno lungo la direzione orizzontale il problema potrebbe essere indeterminato dal momento che possono essere rappresentati infiniti cerchi di Mohr partendo dallo sforzo verticale. Nell’ipotesi di un piano campagna coincidente con il pelo libero ad una certa quota z si ha:
![\[ \sigma_{v0}=\gamma\cdot z \sigma_{h0}=K_{0}\cdot\sigma_{v0}=K_{0}\cdot\gamma\cdot z \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-ec86735f0ed72723dce1916775f22252_l3.png "Rendered by QuickLaTeX.com")
Il coefficiente di spinta passiva K0 può essere valutato con delle prove in sito o valutato per via empirica. K0 per i terreni normalconsolidati (solitamente indicato col simbolo K0(NC)) varia generalmente tra 0.4 e 0.8; in genere si hanno valori più bassi per terreni granulari, più alti per limi e argille. Per terreni coesivi NC, le relazioni empiriche esistenti in letteratura legano generalmente K0 a Ip, con K0 linearmente crescente con Ip.
In generale, per tutti i tipi di terreno, viene spesso utilizzata la seguente relazione di Jaky semplificata: dove φ’ è l’angolo di resistenza al taglio. Per terreni sovraconsolidati, K0 può raggiungere valori anche maggiori di 1, e può essere stimato a partire dal valore di K0 del medesimo terreno normalconsolidato, mediante una relazione del tipo:
![\[ K_{0}(OC)=K_{0}(NC)\cdot OCR^{\alpha} \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-7e02fe96afaee44912a6b7cab7af6f69_l3.png "Rendered by QuickLaTeX.com")
dove α è un coefficiente empirico legato alla natura del terreno e OCR è il grado di sovraconsolidazione.
Per terreni coesivi viene spesso assunto α ≅ 0.5 oppure la formulazione di Terzaghi pari a:
![\[ K_{0}=\frac{\nu}{1-\nu} \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-b2ea38456a3a7fa43f0baa8a9a981be5_l3.png "Rendered by QuickLaTeX.com")
Stato limite attivo
Vediamo come determinare le spinte del terreno sul nostro manufatto.
Nel caso di stato limite attivo si fanno riferimento le ipotesi di Rankine (parete liscia verticale e terrapieno con superficie orizzontale):
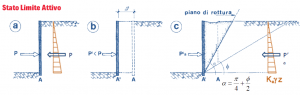
- tensione verticale
![\[ \sigma_{vo}=\gamma\cdot z \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-e94cea4dcf500cb047022a5255625941_l3.png "Rendered by QuickLaTeX.com")
- tensione orizzontale (terreni non coesivi)
![\[ \sigma_{ho}=K_{p}\cdot\sigma_{vo}=K_{p}\cdot\gamma\cdot z \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-de6165fc5be9dcefe0ba1ec02a0bf9b3_l3.png "Rendered by QuickLaTeX.com")
- tensione orizzontale (terreni coesivi)
![\[ \sigma_{ho}=K_{p}\cdot\sigma_{vo}+2c\sqrt{K_{p}} \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-899ef03265f4d76aa812aa4cf2840ffb_l3.png "Rendered by QuickLaTeX.com")
- Spinta Passiva
![\[ P_{p}^{''} \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-d830c8851145a09b131593b1bb925bc3_l3.png "Rendered by QuickLaTeX.com")
- Coefficiente di Spinta Passiva
![\[ K_{p}=\tan^{2}(\frac{\pi}{4}+\frac{\phi}{2}) \]](https://www.soft.lab.it/wp-content/ql-cache/quicklatex.com-fe0e72c529628db833fa2c1135d5b876_l3.png "Rendered by QuickLaTeX.com")
Stato limite passivo
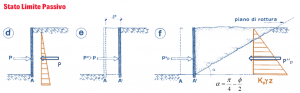
- tensione verticale
- tensione orizzontale (terreni non coesivi)
- tensione orizzontale (terreni coesivi)
- Spinta Passiva
- Coefficiente di Spinta Passiva
Influenza dell’entità degli spostamenti
Le deformazioni di espansione necessarie per far decadere la pressione orizzontale dal valore σ’h0 al valore limite inferiore σ’ha, sono piccole e comunque molto inferiori alle deformazioni di compressione necessarie per far elevare la pressione orizzontale dal valore σ’h0, al valore limite superiore σ’hp. Per il calcolo della spinta attiva si considera l’angolo di resistenza al taglio di picco; per il calcolo della spinta passiva l’angolo di resistenza al taglio a volume costante.
Scopri Monolith 3, il software di calcolo strutturale agli elementi finiti per il calcolo delle opere di sostegno rigide secondo le NTC 2008, NTC 2018 ed Eurocodici.
