Verifica a punzonamento: le indicazioni di Normativa

La rottura per punzonamento è una crisi per taglio di tipo locale che avviene in presenza di carico concentrato molto elevato che agisce su un’area molto piccola, detta area caricata. Il comportamento che si determina non è più schematizzabile come monodimensionale ma si vengono a determinare delle vere e proprie superfici di rottura (comportamento bidimensionale). L’area di trasferimento degli sforzi, per effetto del carico concentrato, viene definita area critica, e le verifiche devono essere effettuate lungo il suo perimetro, detto perimetro critico (Figura 1). L’area critica si determina in base all’area caricata e tenendo conto che l’angolo di diffusione degli sforzi è pari a 26.6° rispetto alla superficie orizzontale della soletta, così come indicato dagli Eurocodici.

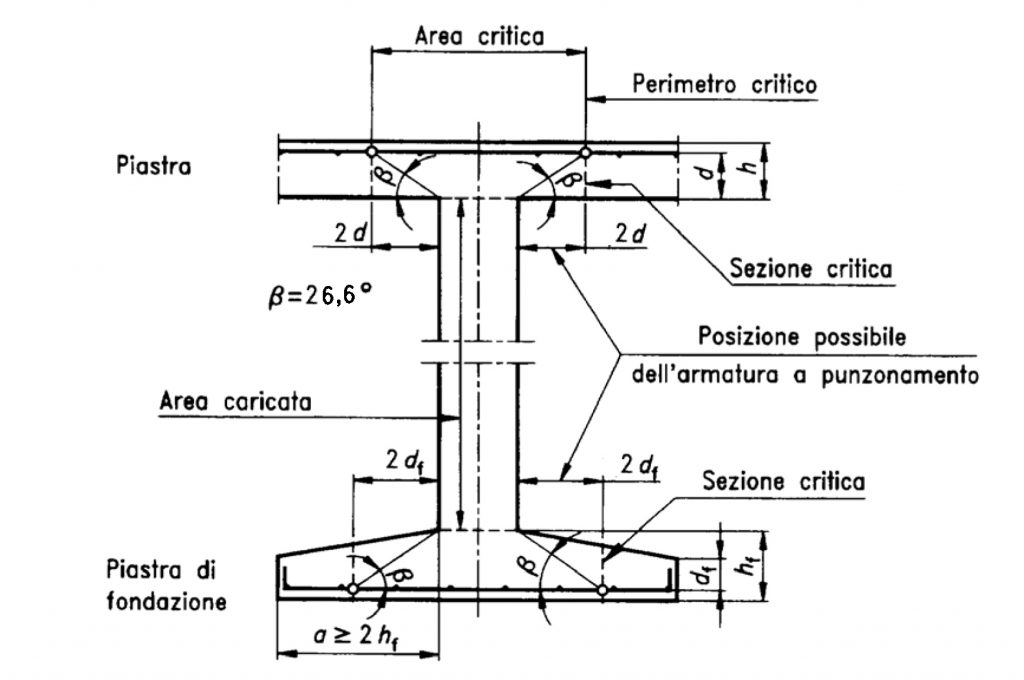
Figura 1. Area caricata, area critica e perimetro critico

Le NTC 2018, al capitolo 4, stabiliscono che: Solette piene, solette nervate a sezione piena sopra le colonne, e fondazioni devono essere verificate nei riguardi del punzonamento allo stato limite ultimo, in corrispondenza dei pilastri e di carichi concentrati. […] Per la valutazione della resistenza al punzonamento si può fare utile riferimento al § 6.4.4 della norma UNI EN1992-1-1 nel caso di assenza di armature al taglio, al § 6.4.5 della norma UNI EN1992-1-1 nel caso di presenza di armature al taglio.
Per procedere alla definizione della resistenza a punzonamento, secondo le formulazioni previste dall’EC2, è necessario individuare il perimetro critico, definito come il perimetro che circonda l’area caricata ad una distanza pari a 2d, essendo d l’altezza utile della piastra.

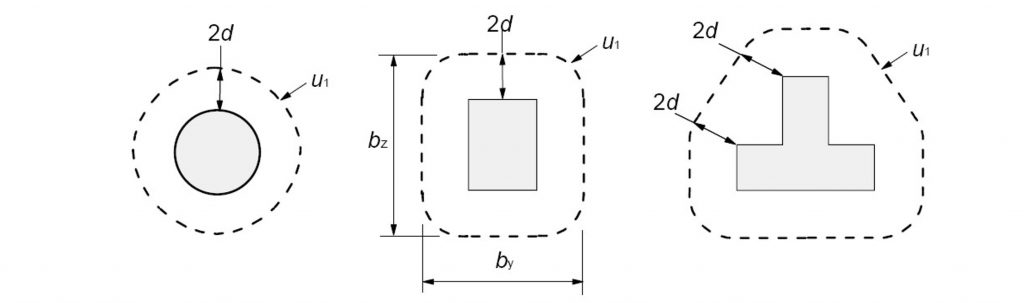
Figura 2. Individuazione del perimetro critico

Ai fini delle verifiche è necessario considerare due schemi di riferimento:

il primo relativo all’area caricata di perimetro u₀;
il secondo relativo all’area critica, o di controllo, di perimetro u₁.

La valutazione delle sollecitazioni tangenziali da punzonamento e le resistenze devono essere valutate sia in corrispondenza del perimetro u₀ che u₁. Ciò significa che è necessario soddisfare le verifiche sia in una configurazione che nell’altra.

Calcolo della sollecitazione da punzonamento

La sollecitazione da taglio-punzonamento v_Sd, in ipotesi di distribuzione plastica delle tensioni, è data dal rapporto tra la forza sollecitante la piastra N_Sd e la superficie di crisi, di area pari u_i·d:

$v_{Sd}=\beta\frac{N_{Sd}}{u_{i}\cdot d}$

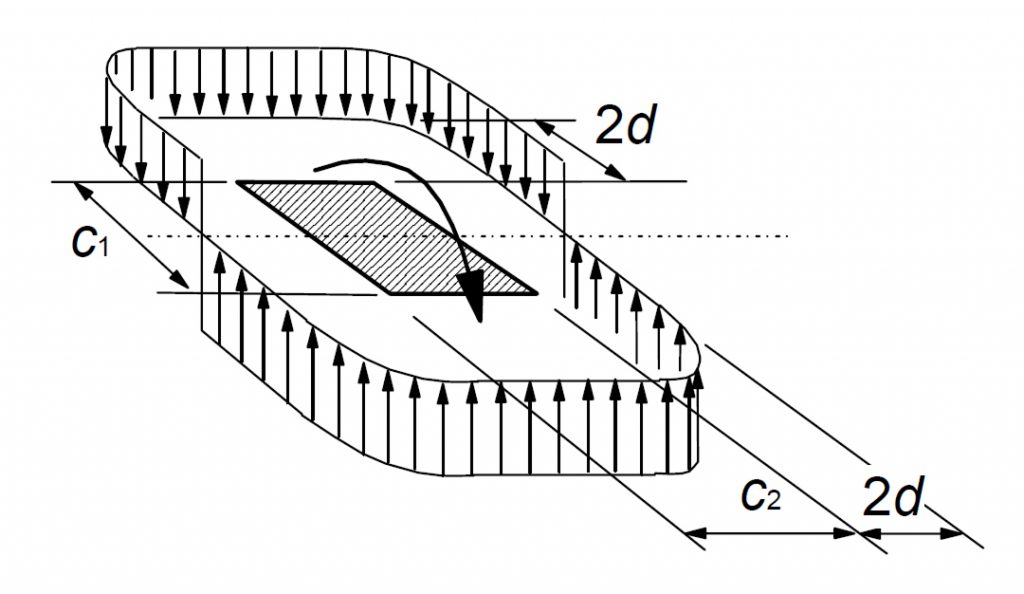
β, invece, è un coefficiente correttivo che tiene conto dell’eventuale eccentricità dello sforzo normale rispetto all’area caricata; in quest’ultimo caso, all’azione trasversale si accompagna anche quella flessionale M_Sd= e·N_Sd.

$\beta=1+k\frac{M_{Sd}}{N_{Sd}}\cdot\frac{u_{i}}{W_{i}}$

k è un fattore riduttivo che dipende dalle dimensioni del pilastro, W_i è il modulo di resistenza plastico del perimetro di controllo.

Nel caso di aree caricate di forma rettangolare, il parametro k può essere dedotto dalla seguente tabella, in funzione del rapporto dei lati c₁ (parallelo all’eccentricità) e c₂(perpendicolare all’eccentricità).

Il modulo di resistenza plastico W₁, relativo ad una sezione critica rettangolare vale:

$W_{1}=\frac{c_{1}^{2}}{2}+c_{1}c_{2}+4dc_{2}+2\pi dc_{1}+16d^{2}$

Figura 3. Sezione rettangolare con carico eccentrico

Nel caso di sezione circolare di diametro D l’espressione di β si presenta nella forma:

$\beta=1+0.6\pi\frac{e}{\left(D+4d\right)}$

Verifica a punzonamento

Come stabilito dalle NTC “in mancanza di un’armatura trasversale appositamente dimensionata, la resistenza al punzonamento deve essere valutata utilizzando formule di comprovata affidabilità, sulla base della resistenza a trazione del calcestruzzo”. La resistenza a punzonamento, nel caso in cui è assente un’apposita armatura, può essere valutata con la seguente formula di natura sperimentale proposta dall’EC2:

$v_{Rd}=\frac{0.18}{\gamma_{c}}\cdot\xi\cdot\left(100\rho_{l}f_{ck}\right)^{1/3}+0.10\cdot\sigma_{cp}\geq0.035\cdot\xi^{3/2}\cdot\sqrt{f_{ck}}+0.10\cdot\sigma_{cp}$

dove:

ξ è pari a 1+(200/d)^0.5
ρ_lè la percentuale geometrica di armatura longitudinale nelle due direzioni, valutate per una lunghezza pari a quella della colonna aumentata di 3d;
f_ck è la resistenza caratteristica del calcestruzzo;
σ_cp è la tensione agente in corrispondenza del perimetro di controllo per effetto di azioni esterne o precompressioni.

La verifica consiste nel controllare che risulti:

$v_{Rd}>v_{Sd}$

Qualora ciò non avvenga è necessario prevedere la presenza di armatura, così come indicato in normativa: “se, sulla base del calcolo, la resistenza a trazione del calcestruzzo sul perimetro efficace non è sufficiente per fornire la richiesta resistenza al punzonamento, vanno inserite apposite armature al taglio. Queste armature vanno estese fino al perimetro più esterno sul quale la resistenza a trazione del calcestruzzo risulta sufficiente.“

Scopri di più sulle soluzioni software per il calcolo strutturale e la geotecnica previste da Soft.Lab , scrivendo a comunicazione@soft.lab.it o telefonando allo 0824 87 43 92.

Resta sempre aggiornato e segui le nostre pagine Facebook, Linkedin, Instagram e YouTube per non perdere le ultime novità!

Verifica a punzonamento: le indicazioni di Normativa

Lascia un commento Annulla risposta

SOFTWARE PER IL CALCOLO STRUTTURALE E LA GEOTECNICA