Duttilità delle sezioni in cemento armato secondo le NTC 2018

Una delle principali novità delle NTC 2018 riguarda le verifiche di duttilità delle sezioni in cemento armato. L’attenzione di questo focus è sulla determinazione della curvatura e quindi la duttili­tà della sezione al variare delle armature tese e compresse, sia per elementi inflessi quali travi e sia per elementi presso inflessi quali i pilastri; si pone come condizione necessaria quella di rispettare i limiti di normativa dei dettagli costruttivi quali geometrie e limiti massimi e minimi per le armature longitudinali e trasversali.

Nel Capitolo 7, al Par. 7.3.6 denominato Rispetto dei requisiti nei confronti degli stati limite, si fa riferimento alle verifiche da effettuare su elementi strutturali, non strutturali ed impianti ed in particolare alla Tab. 7.3.III si riporta, in casi specifici esplicitati dalle NTC 2018, l’obbligatorietà della verifica di duttilità.

Tale controllo si rende obbligatorio per le parti strutturali:

• nel caso di analisi lineare, coerente con il fattore di comportamento q adottato e i relativi spostamenti, quali definiti in 7.3.3.3;
• nel caso di analisi non lineare, sufficiente a soddisfare la domanda in duttilità evidenziata dall’analisi.

Per strutture a comportamento dissipativo, qualora non siano rispettate le regole specifiche dei dettagli costruttivi, come previsto dalla Norma, occorrerà procedere a verifiche di duttilità.

Per le sezioni allo spiccato dalle fondazioni o dalla struttura scatolare rigida di base di cui al § 7.2.1 degli elementi strutturali verticali primari la verifica di duttilità, indipendentemente dai particolari costruttivi adottati, è necessaria (salvo casi diversi esplicitati dalle NTC 2018) accertando che la capacità in duttilità della costruzione sia almeno pari:

• a 1,2 volte la domanda in duttilità locale, valutata in corrispondenza dello SLV, nel caso si utilizzino modelli lineari,
• alla domanda in duttilità locale e globale allo SLC, nel caso si utilizzino modelli non lineari.

Le verifiche di duttilità non sono dovute nel caso di progettazione con q ≤ 1,5.

Nel caso in esame, si ipotizza una struttura con un fattore di comportamento q > 1,5.

Si procede con l’analisi della duttilità. Come previsto dalle NTC 2018, la verifica consiste confrontando la capacità (espressa in termini di duttilità) e la domanda.

Valutazione della capacità

La capacità in termini di duttilità, si valuta secondo quanto previsto dal Capitolo 4, Par. 4.1.2.3.4.2 secondo le relazioni:

• è il valore di progetto del momento resistente corrispondente a ;
• è il valore di progetto dello sforzo normale sollecitante;
• è il valore di progetto del momento di domanda;
• è il valore di progetto della duttilità di curvatura corrispondente a ;
• è la domanda in termini di duttilità di curvatura.

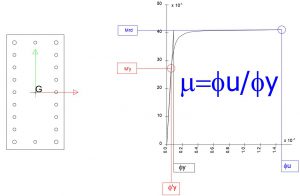
La capacità in termini di fattore di duttilità in curvatura può essere calcolata, separatamente per le due direzioni principali di verifica, come rapporto tra la curvatura cui corrisponde una riduzione del 15% della massima resistenza a

flessione – oppure il raggiungimento della deformazione ultima del calcestruzzo e/o dell’acciaio – e la curvatura convenzionale di prima plasticizzazione espressa dalla relazione seguente:

dove:
– è la minore tra la curvatura calcolata in corrispondenza dello snervamento dell’armatura tesa e la curvatura calcolata in corrispondenza della deformazione di picco ( se si usa il modello parabola-rettangolo oppure se si usa il modello triangolo-rettangolo) del calcestruzzo compresso;
– è il momento resistente della sezione allo SLU;
– è il momento corrispondente a e può essere assunto come momento resistente massimo della sezione in campo sostanzialmente elastico.

Valutazione della domanda

La domanda in duttilità di curvatura allo SLC nelle zone dissipative, espressa mediante il fattore di duttilità in curvatura , qualora non si proceda ad una determinazione diretta mediante analisi non lineare, può essere valutata in via approssimata come:

dove è il periodo proprio fondamentale della struttura.
La capacità in duttilità di curvatura può essere calcolata come indicato al § 4.1.2.3.4.2.

Verifica di duttilità

Per le zone dissipative allo spiccato dei pilastri primari e per le zone terminali di tutti i pilastri secondari devono essere eseguite le verifiche di duttilità indicate al § 7.4.4.2.2. In alternativa, tali verifiche possono ritenersi soddisfatte se, per ciascuna zona dissipativa, si rispettano le limitazioni seguenti:

dove:
– è il rapporto meccanico dell’armatura trasversale di confinamento all’interno della zona dissipativa (il nucleo di calcestruzzo è individuato con riferimento alla linea media delle staffe) che deve essere non minore di 0,12 in CD”A” .
– è la domanda in duttilità di curvatura allo SLC;
– è la forza assiale adimensionalizzata di progetto relativa alla combinazione sismica SLV ( = ∙);
– è la deformazione di snervamento dell’acciaio;
– è la profondità della sezione trasversale lorda;
– è la profondità del nucleo confinato (con riferimento alla linea media delle staffe);
– è la larghezza minima della sezione trasversale lorda;
– è la larghezza del nucleo confinato corrispondente a bc (con riferimento alla linea media delle staffe);
– è il coefficiente di efficacia del confinamento, uguale a = ∙, con variazione a seconda della tipologia di sezione.

Acquista IperSpace BIM il software di calcolo strutturale BIM oriented per il calcolo di strutture in cemento armato, acciaio, legno e miste compatibile con le NTC 2018.