Elementi shell: come ottimizzare il passo della mesh e velocizzare il calcolo

La modellazione delle strutture intelaiate richiede l’utilizzo di elementi asta, ovvero elementi monodimensionali per i quali vale la teoria della trave elastica di Timoschenko. Capita spesso però che gli elementi strutturali di un edificio non possano essere schematizzati utilizzando solo elementi monodimensionali. Ci sono elementi strutturali che devono per forza essere modellati ricorrendo all’utilizzo di elementi bidimensionali quali:

• Pareti in cemento armato (elementi caratterizzati da un rapporto fra dimensione massima e minima della sezione maggiore di 4);
• Muri di contenimento dei piani interrati;
• Platee di fondazione;
• Solai a piastra a soletta piena;

La corretta analisi di questi elementi strutturali richiede la modellazione attraverso elementi shell. L’inserimento di elementi shell nel modello strutturale porta il progettista di fronte ad una scelta da compiere: quale passo di discretizzazione utilizzare per la creazione della mesh di questi elementi? Prediligere la velocità del calcolo o l’accuratezza? 

L’articolo di seguito riportato dal titolo “Elementi shell: come ottimizzare il passo della mesh e velocizzare il calcolo” è a cura di Marco De Pisapia, ingegnere civile e autore del blog www.marcodepisapia.com dove da oltre tre anni pubblica ogni settimana un nuovo articolo di approfondimento sul tema dell’analisi e del calcolo strutturale. I temi affrontati nello specifico sono:

• come si classificano gli elementi bidimensionali piani e quali sono i metodi di analisi utilizzati dai software di calcolo;
• come discretizzare nel modo giusto gli elementi bidimensionali e quale dimensione della mesh scegliere per ottimizzare i tempi di risoluzione senza perdere in accuratezza;
• gli errori da non commettere quando si creano elementi bidimensionali;
• un caso studio relativo ad una struttura multipiano con 15562 elementi piani e 92280 gradi di libertà.

L’analisi degli elementi bidimensionali: un compromesso fra accuratezza dei risultati e tempi di risoluzione

L’analisi degli elementi bidimensionali è più complessa rispetto all’analisi degli elementi monodimensionali utilizzati per la modellazione di travi e pilastri. Grazie alle notevoli capacità di calcolo dei pc, oggi non è un problema affrontare l’onere computazionale che comporta l’utilizzo di elementi bidimensionali, ottenendo una notevole accuratezza dei risultati, modellando correttamente questi elementi e scegliendo il giusto passo di discretizzazione. Per poter correttamente modellare e discretizzare gli elementi bidimensionali è fondamentale per un progettista conoscere i metodi di risoluzione che utilizza un software di calcolo e i princìpi del comportamento statico di tali elementi. La corretta discretizzazione di questi elementi è un passo fondamentale per evitare il rischio di allungare notevolmente i tempi di risoluzione.

Comportamento a lastra, a piastra e a guscio (shell)

Prima di passare in rassegna il metodo di analisi utilizzato dai software di calcolo per il calcolo degli elementi bidimensionali, si riportano i tre tipi di comportamento di questi elementi:

• comportamento a lastra: ciascun nodo dell’elemento possiede due gradi di libertà ovvero due traslazioni nel piano dell’elemento. Viene utilizzato per rappresentare stati di sforzo piano e le azioni sollecitanti giacciono nel piano dell’elemento. È un elemento dotato di rigidezza membranale e trasmette solo sforzi nel suo piano;
• comportamento a piastra: ciascun nodo di quest’elemento è dotato di tre gradi di libertà, una traslazione ortogonale al piano medio dell’elemento e due rotazioni intorno ai due assi appartenenti al piano dell’elemento. È un elemento dotato di rigidezza flessionale e trasmette sollecitazioni taglianti e flessionali. Le azioni sollecitanti sono ortogonali al piano dell’elemento.
• l’elemento shell (guscio) è la sovrapposizione dei due comportamenti a lastra e piastra appena visti. È un elemento dotato di rigidezza sia flessionale che membranale e può essere utilizzato per riprodurre il comportamento generico di un elemento strutturale piano.

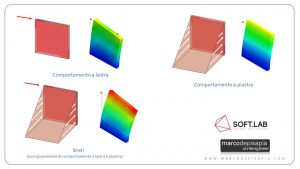
Fig.1: Tipologie di comportamento degli elementi piani

L’analisi agli Elementi Finiti degli elementi piani (FEM method analysis)

Le deformazioni e le tensioni degli elementi bidimensionali sotto assegnate condizioni di carico, vengono determinate attraverso il Metodo degli Elementi Finiti. L’elemento shell viene discretizzato in una mesh di elementi di forma triangolare o quadrangolare, connessi in corrispondenza dei nodi. Le incognite del problema diventano pertanto gli spostamenti dei nodi degli elementi che compongono la mesh. Gli spostamenti dei punti all’interno di ciascun elemento vengono ipotizzati essere funzione degli spostamenti nodali attraverso funzioni lineari o non lineari a seconda della tipologia di elemento di discretizzazione adottato. Noti gli spostamenti di ciascun nodo dell’elemento, si può risalire alle deformazioni e, attraverso la matrice di rigidezza, alle tensioni.

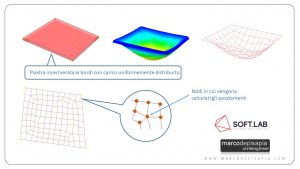
Fig.2: Nodi della mesh di un elemento shell

Come trovare la giusta dimensione della mesh: il modello ad infittimento crescente

L’accuratezza del risultato in termini di deformazioni e tensioni di un elemento bidimensionale, dipende dalla dimensione dei singoli elementi che compongono la mesh. Più fitta è la discretizzazione, più accurati saranno i risultati. Di contro però saranno più lunghi i tempi di risoluzione in quanto all’aumentare dei nodi dell’elemento aumenterà la dimensione della matrice di rigidezza. Per zone in cui il gradiente di deformazione e tensione è più elevato, è bene infittire la mesh. Ciò accade in corrispondenza di zone critiche dell’elemento quali: spigoli, fori, discontinuità, cambi di sezione, applicazione di carichi concentrati. All’interno di uno stesso elemento shell si può adottare un diverso infittimento della mesh. I software di calcolo sono solitamente dotati di un algoritmo automatico che crea la mesh dell’elemento sulla base del passo scelto. In IperSpace BIM tale procedura è automatizzata e il progettista può scegliere il passo della mesh e se raffinare o meno il reticolo.

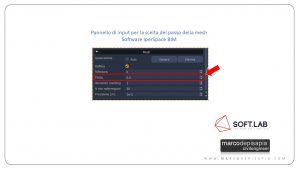
Fig.3: Pannello di controllo in IperSpace BIM per la scelta del passo della mesh e l’attivazione dell’opzione Raffina per ottimizzare la forma degli elementi

Per quanto i software di calcolo possano automatizzare la procedura di creazione della mesh di elementi bidimensionali, spetta comunque al progettista la scelta del passo di discretizzazione della mesh. Per controllare l’accuratezza dei risultati ottenuti e valutare se il passo scelto consente di ottenere risultati affidabili, si può adottare una procedura ad infittimento crescente e confrontare i risultati ottenuti. Tale procedura consiste nell’eseguire il calcolo con passi della mesh via via decrescenti e vedere di quanto variano i risultati. Il passo corretto sarà quello che determina variazioni trascurabili dei risultati e tempi di risoluzione accettabili.

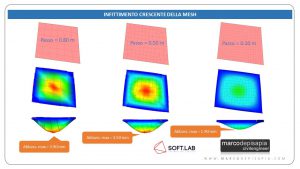
Fig.4: Convergenza della soluzione in funzione del numero di elementi che compone la mesh

Gli errori da evitare: elementi allungati, mesh distorte, incongruenza fra nodi

Ci sono alcuni princìpi da seguire nel controllo visivo dell’affidabilità di una mesh:

• il rapporto fra i lati degli elementi (aspect ratio) deve essere quanto più vicino possibile all’unità;
• gli angoli ai vertici dei singoli elementi dovrebbero assumere valori fra loro vicini: 90° per elementi quadrangolari e 60° per elementi triangolari;
• infittimento della mesh in corrispondenza delle zone critiche, ovvero le zone con alti gradienti di tensione e deformazione.

Se non vengono rispettati questi principi si rischia di compromettere l’affidabilità del risultato.

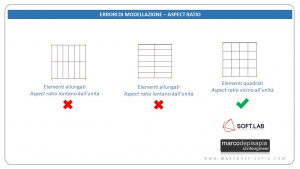
Fig.5: Aspect ratio di elementi quadrangolari

Un altro errore da evitare riguarda l’incongruenza fra i nodi di due elementi piani collegati fra loro o l’eccessiva distorsione di un elemento. Ciò si verifica quando:

• i due elementi hanno un diverso passo di discretizzazione con conseguente incongruenza fra i nodi;
• la mesh non si collega ad un nodo che giace sul nel suo piano, per esempio il nodo di base di un pilastro che è stato creato dopo la creazione della mesh della platea di fondazione.
• Elementi eccessivamente distorti, con lati e angoli ai vertici molto disuguali fra loro.

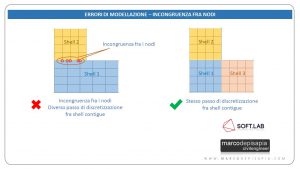
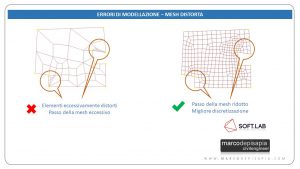
Fig.6: Incongruenza fra nodi e mesh distorta

Un caso studio: una struttura a pareti con solai a piastra, minimizzare i tempi di calcolo

Si riporta di seguito un caso studio che riguarda il modello strutturale di un edificio in cui le shell rappresentano la quasi totalità degli elementi strutturali. La struttura è stata concepita nel modo seguente:

• solai a piastra realizzati con soletta piena;
• pareti sismoresistenti;
• fondazione a platea.

I pochi pilastri presenti nella struttura sono stati progettati come elementi secondari, ovvero assorbono solo i carichi verticali, ma non danno contributo alla resistenza nei confronti delle azioni orizzontali. L’aliquota di tagliante sismico assorbito dai pilastri è inferiore al 20%. Considerando che l’edificio è composto da undici livelli fuori piano, bisogna porre attenzione al passo della mesh che si sceglie di utilizzare per discretizzare gli elementi bidimensionali. A causa dell’elevato numero di nodi, si rischierebbe di avere tempi di elaborazione lunghissimi. Per fissare un corretto passo della mesh si possono fare le seguenti valutazioni: le mesh dei solai possono essere discretizzate con un passo non molto fitto, in quanto si vuole riprodurre solo l’effettiva rigidezza nel piano di tali elementi (non è stato modellato l’impalcato rigido). La verifica dei solai sarà eseguita in un modello ad hoc in cui si analizza il solo solaio, adottando un passo più fitto della mesh al fine di ottenere risultati più affidabili in termini di spostamenti verticali e sollecitazioni.

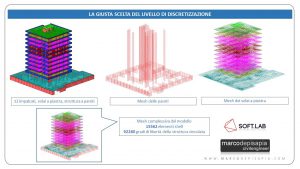
Fig.7: Caso studio: modello di una struttura a pareti con solai a piastra

Conclusioni

Se sceglie di progettare una struttura con pareti sismoresistenti e solai a piastra occorre modellare degli elementi shell per riprodurre il comportamento strutturale dell’edificio. Lo stesso accade nel caso dell’utilizzo di platee di fondazione. La massima cura va posta nella scelta del passo di discretizzazione al fine di ottenere risultati affidabili e tempi di risoluzione modesti. Particolare attenzione va posta ai tempi di risoluzione. In fase di progetto è fondamentale ridurli al massimo. La progettazione è una procedura iterativa. Si consideri ad esempio che un modello impieghi circa 40 minuti per completare il calcolo e a conclusione del procedimento vi siano degli elementi non verificati. In tal caso occorre rimodificare il modello e far girare di nuovo il calcolo. Attraverso queste iterazioni. lunghi tempi di risoluzione possono rallentare di molto la procedura. Il consiglio è quello di adottare una mesh iniziale non molto fitta. Se tutte le verifiche risultano soddisfatte, affinare il modello riducendo il passo della mesh.